The
concept of discrete timing is applied to the S/E nets as follows: to every
pre-arc [p,t] of the transition t we attach an interval [l,h]
of natural numbers with 0 < l < h <¥.
The interval is also referred to as
permeability interval. If a pre-arc has no explicitly designated
permeability interval, it is assumed to be [0, ¥
]. The interpretation is as follows. Every place p bears a clock u(p)
which is running iff the place is marked (m(p)>0) and switched
off otherwise. All running clocks run at the same speed measuring the time the
token status of its place has not been changed. If a firing transition t
removes a token from the place p or adds a token to p, the clock
of p is turned back to 0. A (marking-enabled) transition t is time-enabled
only if for any pre-place p of t the clock at place p shows
a time u(p) such that l(p,t) < u(p) < h(p,t).
A
state is characterized by the marking of system plus the positions of the local
clocks at the places. A state is called dead if no transition is
time-enabled and no transition would become able to fire after any increments of
the clocks. If in state
there is such a minimum increment
that some of the transitions become
enabled after elapsing it, then it is said that the state transition
has a “delay”
. Conversely, it can be interpreted as the state
has a “duration”
, that specifies the time increment of the clocks of this state required to make
the transition
enabled.
At a
given state all (time-)enabled steps have to be computed and placed into the
list of enabled steps. Firing of each step brings one more state successor to
the current state. Repetitive application of this procedure to every subsequent
state forms the reachability space of the model. Time-enableness is a required
but not sufficient condition to include transition to the firing step. The
interpretation of the timing intervals is defined by the timing firing rule.
Several such rules have been studied:
1.
Strong vs. weak firing:
with the strong rule all marking enabled (spontaneous) transitions, which
have pre-places with clock position equal
to either low or high time limit, are obligatorily inserted into the step (can
be specified to make e.g. either strong earliest firing rule, or strong latest
firing rule). If the weak rule is chosen then at least one of the enabled
spontaneous transitions has to be included in step.
2. Earliest vs.
interval firing:
In case of the interval firing a transition is time-enabled at every
clock position within the interval [l,h]. In the earliest firing
rule a transition is time-enabled if it has a pre-place with the clock value
equal to the low bound l of the time interval.
3.
Ultimo
firing: is a
certain combination of the interval and strong rules: a transition is time-enabled every time tick within the
interval and must fire at the latest at clock position equal to h.
It is
necessary to mention that in case a transition has several incoming arcs with
permeability intervals [l1,h1],[l2,h2],…[ln,hn]
then all arcs have to be permeable for the firing, that means l=max(li),h=min(hi).
Among all possible combinations of time constants and time-firing rules, some
were found of interest in some industrial applications. These combinations are
presented in Table 1.
|
|
Time
constants |
Firing
rule |
Interpretation |
|
1. |
l>0,h
³
l |
Interval,
weak |
Event
is expected with minimum delay l, maximum delay h, or may
not occur at all. |
|
2. |
l>0,h
³
l |
Ultimo |
Process must get terminated within the interval [l,h] |
|
3. |
l>0,h=¥ |
Earliest,
strong |
Process has duration l, and all simultaneously
started processes with the same duration finish simultaneously |
|
4. |
l>0,h=¥ |
Earliest,
weak |
Process has duration l, but termination of all
processes with the same duration may be not synchronized . |
Table 1. Combinations of time-firing rule and time intervals commonly used for modeling.
The lower or higher time limits may or may not (depending on the corresponding rule) force transition to fire. The "interval" firing rule accepts presence of empty transition steps, when time elapses even in the absence of any enabled transitions. This option may be useful if aimed at finding of all possible combinations of overlapping processes and, correspondingly, simultaneous events. On the other hand it obviously explodes the reachability space. The variety of choices is maybe confusing, but it extends the modeling horizons and allows more concise description of models. The following example explains the differences between firing options.
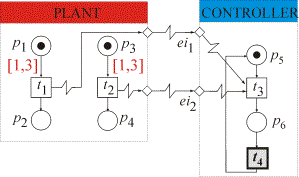
Figure 1. Timed version of plant-controller interaction
The following state-time diagrams illustrate different combinations of timed firing options. The earliest strong firing rule forces to fire all transitions when the low time bound is reached by clocks, at the earliest weak rule steps are formed from combinations of time-enabled transitions, at ultimo the firing may occur at every discrete time value within the permeability interval.
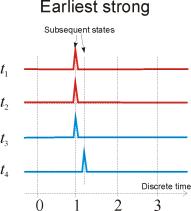
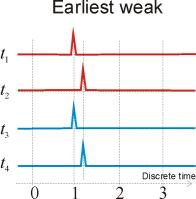
Figure
2. State-time diagrams representing different combinations of timed firing
options.
© 2003,
Martin
Luther University of Halle-Wittenberg, Automation Technology
Lab.
Recommended
browser: IE4.0 or higher
Document created and maintained by: Valeriy V. Vyatkin