 b).
b).
Discrete formalisms with discrete time are limited in precision of the given results for obvious reasons if compared with description of the system using hybrid formalisms. However, in exchange they offer better complexity estimations.
To be really useful for verification purposes the model of plant must have its own dynamics, i.e. generate events, and respond to interaction from the controller as the real plant would. Spontaneous transitions in the model of plant model different non-determined or multi-choice actions. If several such transitions are enabled it reflects the situation when several simultaneous processes take part. When these are combined with the model of controller, each of the processes draws the corresponding reaction of the controller. Processes in discrete modeling are represented as states. Each stable state can be also explicitly associated with duration.
Underlying
(sub-)processes which represent on
abstract levels (sub-) states of the model can be modeled in S/E nets as places with
safe (0/1) marking. Each stable state can be also explicitly associated with a
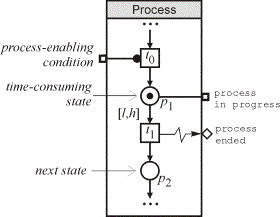
duration. Figure 1,a shows an
example of such a model. The time consuming state, represented by p1,
models an action in progress. Transition t0 has an incoming
condition arc which starts the process. The process is in progress while p1
is marked. Permeability interval of the arc (p1,t1)
defines the duration of the process in one of the ways described in the previous
section.
a).
 b).
b).

Figure
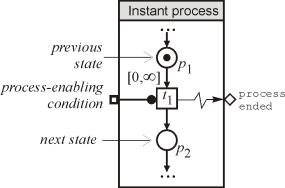
1. a) Model of plain time consuming process; b) Model of instant process.
There
are some processes which have no duration, or it can be neglected in comparison
to other ones. Such processes are called "instant". An example of a
model of such a process is given in Figure 1,b. The process is started by
"enabling condition", but there is no place marking corresponding to
the state "process in progress".
More
realistic modeling of processes (as the one shown in Figure 2) may include
exception states in which the system comes in case of abnormal process
termination. The place p1 (modeling the time-consuming state
as in the previous example) is connected with two transitions: t1
stands for the normal operation mode with a duration as described in the
previous case, while t2 models the exception state, which may
occur anytime within the normal operation time. This model is most adequate with
the "ultimo" firing rule and h < ¥.
The reached upper time limit forces only one of the transitions: either ending
the action normally, or exceptionally.
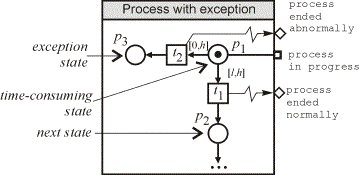
Figure 2. Model of process with a possible exception.
© 2003,
Martin
Luther University of Halle-Wittenberg, Automation Technology
Lab.
Recommended
browser: IE4.0 or higher
Document created and maintained by: Valeriy V. Vyatkin